Python Set and Booleans with Syntax and Examples

So far, we have learned about various data types in Python. We dealt with strings, numbers, lists, tuples, and dictionaries.

We’ve also learned that we don’t need to declare the type of data while defining it. Today, we will talk about Python set examples and Python Booleans.

After that, we will move on to Python functions in further lessons.

What are Sets in Python?

First, we focus on Python sets. A set in Python holds a sequence of values. It is sequenced but does not support indexing.

We will understand that as we get deeper into the article with the Python set Examples.

1. Creating a Python Set

To declare a set, you need to type a sequence of items separated by commas, inside curly braces. After that, assign it to a Python variable.

>>> a={1,3,2}

As you can see, we wrote it in the order 1, 3, 2. In point b, we will access this set and see what we get back.

A set may contain values of different types.

>>> c={1,2.0,'three'}

a. Duplicate Elements

A set also cannot contain duplicate elements. Let’s try adding duplicate elements to another set, and then access it in point b.

>>> b={3,2,1,2}

b. Mutability

A set is mutable, but may not contain mutable items like a list, set, or even a dictionary.

>>> d={[1,2,3],4}

Output

As we discussed, there is no such thing as a nested Python set.

>>> d={{1,3,2},4}

Output

You can also create a set with the set() function.

>>> d=set()
>>> type(d)

Output

This creates an empty set object. Remember that if you declare an empty set as the following code, it is an empty dictionary, not an empty set. We confirm this using the type() function.

>>> d={}
>>> type(d)

Output

The set() function may also take one argument, however. It should be an iterable, like a list.

>>> d=set([1,3,2])

2. Accessing a Set in Python

Since sets in Python do not support indexing, it is only possible to access the entire set at once. Let’s try accessing the sets from point a.

>>> a

Output

Did you see how it reordered the elements into an ascending order? Now let’s try accessing the set c.

>>> c

Output

Finally, let’s access set b.

>>> b

Output

As you can see, we had two 2s when we declared the set, but now we have only one, and it automatically reordered the set.

Also, since sets do not support indexing, they cannot be sliced. Let’s try slicing one.

>>> b[1:]

Output

As you can see in the error, a set object is not subscriptable.

3. Deleting a Set in Python

Again, because a set isn’t indexed, you can’t delete an element using its index. So for this, you must use one of the following methods.

A method must be called on a set, and it may alter the set. For the following examples, let’s take a set called numbers.

>>> numbers={3,2,1,4,6,5}
>>> numbers

Output

a. discard() method in Python

This method takes the item to delete as an argument.

>>> numbers.discard(3)
>>> numbers

Output

As you can see in the resulting set, item 3 has been removed.

b. remove() method in Python

Like the discard() method, remove() deletes an item from the set.

>>> numbers.remove(5)
>>> numbers

Output

discard() vs remove():

These two methods may appear the same to you, but there’s actually a difference.

If you try deleting an item that doesn’t exist in the set, discard() ignores it, but remove() raises a KeyError.

>>> numbers.discard(7)
>>> numbers

Output

>>> numbers.remove(7)

Output

c. pop() method in Python set

Like in a dictionary, you can call the pop() method on a set. However, here, it does not take an argument.

Because a set doesn’t support indexing, there is absolutely no way to pass an index to the pop method. Hence, it pops out an arbitrary item.

Furthermore, it prints out the item that was popped.

>>> numbers.pop()

Output

Let’s try popping anot/her element.

>>> numbers.pop()

Output

Let’s try it on another set as well.

>>> {2,1,3}.pop()

Output

d. clear() method in Python set

Like the pop method(), the clear() method for a dictionary can be applied to a Python set as well. It empties the set in Python.

>>> numbers.clear()
>>> numbers

Output

As you can see, it denoted an empty set as set(), not as {}.

4. Updating a Set in Python

As we discussed, a Python set is mutable. But as we have seen earlier, we can’t use indices to reassign it.

>>> numbers={3,1,2,4,6,5}
>>> numbers[3]

Output

So, we use two methods for this purpose- add() and update(). We have seen the update() method on tuples, lists, and strings.

a. add() method in Python set

It takes as an argument the item to be added to the set.

>>> numbers.add(3.5)
>>> numbers

Output

If you add an existing item in the set, the set remains unaffected.

>>> numbers.add(4)
>>> numbers

Output

b. update() method in Python set

This method can add multiple items to the set at once, which it takes as arguments.

>>> numbers.update([7,8],{1,2,9})
>>> numbers

Output

As is visible, we could provide a list and a set as arguments to this. This is because this is different than creating a set.

5. Python Functions on Sets

A function is something that you can apply to a Python set, and it performs operations on it and returns a value. Let’s talk about some of the functions that a set supports.

We’ll take a new set for exemplary purposes.

>>> days={'Monday','Tuesday','Wednesday','Thursday','Friday','Saturday','Sunday'}

a. len() function in Python set

The len() function returns the length of a set. This is the number of elements in it.

>>> len(days)

Output

b. max() function in Python set

This function returns the item from the set with the highest value.

>>> max({3,1,2})

Output

We can make such a comparison on strings as well.

>>> max(days)

Output

The Python function returned ‘Wednesday’ because W has the highest ASCII value among M, T, W, F, and S.

But we cannot compare values of different types.

>>> max({1,2,'three','Three'})

Output

c. min() function in Python set

Like the max() function, the min() function returns the item in the Python set with the lowest value.

>>> min(days)

Output

This is because F has the lowest ASCII value among M, T, W, F, and S.

d. sum() function in Python set

The sum() functionin Python set returns the arithmetic sum of all the items in a set.

>>> sum({1,2,3})

Output

However, you can’t apply it to a set that contains strings.

>>> sum(days)

Output

e. any() function in Python set

This function returns True even if one item in the set has a Boolean value of True.

>>> any({0})

Output

>>> any({0,'0'})

Output

It returns True because the string ‘0’ has a Boolean value of True.

f. all() function in Python set

Unlike the any() function, all() returns True only if all items in the Python set have a Boolean value of True. Otherwise, it returns False.

>>> all({0,'0'})

Output

>>> all(days)

Output

g. sorted() function in Python set

The sorted() function returns a sorted python set to list. It is sorted in ascending order, but it doesn’t modify the original set.

>>> numbers={1, 2, 3, 4, 5, 6, 3.5}
>>> sorted(numbers)

Output

6. Python Methods on Sets

Unlike a function in Python set, a method may alter a set. It performs a sequence on operations on a set, and must be called on it.

So far, we have learned about the methods add(), clear(), discard(), pop(), remove(), and update(). Now, we will see more methods from a more mathematical point of view.

a. union() method in Python set

This method performs the union operation on two or more Python sets. What it does is it returns all the items that are in any of those sets.

Union in Python Set

>>> set1,set2,set3={1,2,3},{3,4,5},{5,6,7}
>>> set1.union(set2,set3)

Output

>>> set1

Output

As you can see, it did not alter set1. A method does not always alter a set in Python.

b. intersection() method in Python set

This method takes as arguments sets, and returns the common items in all the sets.

Intersection Set in Python

>>> set2.intersection(set1)

Output

Let’s intersect all three sets.

>>> set2.intersection(set1,set3)

Output

It returned an empty set because these three sets have nothing in common.

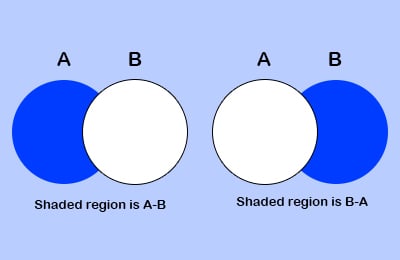
c. difference() method in Python set

The difference() method returns the difference of two or more sets. It returns as a set.

Difference Python Set

>>> set1.difference(set2)

Output

This returns the items that are in set1, but not in set2.

>>> set1.difference(set2,set3)

Output

d. symmetric_difference() method in Python set

This method returns all the items that are unique to each set.

Symmetric difference set in Python

>>> set1.symmetric_difference(set2)

Output

It returned 1 and 2 because they’re in set1, but not in set2. This also returned 4 and 5 because they’re in set2, but not in set1. It did not return 3 because it exists in both the sets.

e. intersection_update() method in Python set

As we discussed in intersection(), it does not update the set on which it is called. For this, we have the intersection_update() method.

>>> set1.intersection_update(set2)
>>> set1

Output

It stored 3 in set1, because only that was common in set1 and set2.

f. difference_update() method in Python set

Like intersection-update(), this method updates the Python set with the difference.

>>> set1={1,2,3}
>>> set2={3,4,5}
>>> set1.difference_update(set2)
>>> set1

Output

g. symmetric_difference_update() method in Python set

Like the two methods we discussed before this, it updates the set on which it is called with the symmetric difference.

>>> set1={1,2,3}
>>> set2={3,4,5}
>>> set1.symmetric_difference_update(set2)
>>> set1

Output

h. copy() method in Python set

The copy() method creates a shallow copy of the Python set.

>>> set4=set1.copy()
>>> set1,set4

Output

i. isdisjoint() method in Python set

This method returns True if two sets have a null intersection.

>>> {1,3,2}.isdisjoint({4,5,6})

Output

However, it can take only one argument.

>>> {1,3,2}.isdisjoint({3,4,5},{6,7,8})

Output

j. issubset() method in Python set

This method returns true if the set in the argument contains this set.

>>> {1,2}.issubset({1,2,3})

Output

>>> {1,2}.issubset({1,2})

Output

{1,2} is a proper subset of {1,2,3} and an improper subset of {1,2}.

k. issuperset() method in Python set

Like the issubset() method, this one returns True if the set contains the set in the argument.

>>> {1,3,4}.issuperset({1,2})

Output

>>> {1,3,4}.issuperset({1})

Output

7. Python Operations on Sets

Now, we will look at the operations that we can perform on sets.

a. Membership operation

We can apply the ‘in’ and ‘not in’ python operators on items for a set. This tells us whether they belong to the set.

>>> 'p' in {'a','p','p','l','e'}

Output

>>> 0 not in {'0','1'}

Output

8. Iterating on a Set in Python

As we have seen with lists and tuples, we can also iterate over a set in a for loop.

>>> for i in {1,3,2}:
        print(i)

Output

As you can see, even though we had the order as 1,3,2, it is printed in ascending order.

9. The frozenset

A frozen set is an immutable set. You cannot change its values. Also, a set can’t be used as a key for a dictionary, but a frozenset can.

Characteristics of frozenset in Python:

• Immutable: Once the frozenset is formatted, you cannot add, remove, or change the elements.
• Hashable: Frozen sets are different from other sets as they act as a key in dictionaries or an element in another set.
• Unordered: They do not have their specific positions.
• Unique feature: It has the ability to remove duplicate data entries.

>>> {{1,2}:3}

Output

Now let’s try doing this with a frozenset.

>>> {frozenset(1,2):3}

Output

As you can see, it takes only one argument. Now let’s see the correct syntax.

>>> {frozenset([1,2]):3}

Output

What are Python Booleans?

Finally, let’s discuss Booleans. A Boolean is another data type that Python has to offer.

1. Value of a Boolean

As we have seen earlier, a Boolean value may either be True or be False. Some methods like isalpha() or issubset() return a Boolean value.

2. Declaring a Boolean

You can declare a Boolean just like you would declare an integer.

>>> days=True

As you can see here, we didn’t need to delimit the True value by quotes. If you do that, it is a string, not a Boolean.

Also note that what was once a set, we have reassigned a Boolean to it.

>>> type('True')

Output

3. The bool() function in Python

Like we have often seen earlier, the bool() function converts another value into the Boolean type.

>>> bool('Wisdom')

Output

>>> bool([])

Output

4. Boolean Values of Various Constructs

Different values have different equivalent Boolean values. In this example, we use the bool() Python set function to find the values.

For example, 0 has a Boolean value of False.

>>> bool(0)

Output

1 has a Boolean value of True, and so does 0.00000000001.

>>> bool(0.000000000001)

Output

A string has a Boolean value of True, but an empty string has False.

>>> bool(' ')

Output

>>> bool('')

Output

In fact, any empty construct has a Boolean value of False, and a non-empty one has

Output

>>> bool(())

Output

>>> bool((1,3,2))

Output

5. Operations on Booleans

a. Arithmetic Operation

You can apply some arithmetic operations to a set. It takes 0 for False, and 1 for True, and then applies the operator to them.

Addition:

You can add two or more Booleans. Let’s see how that works.

>>> True+False #1+0

Output

>>> True+True #1+1

Output

>>> False+True #0+1

Output

>>> False+False #0+0

Subtraction and Multiplication:

The same strategy is adopted for subtraction and multiplication.

>>> False-True

Output

Division:

Let’s try dividing Booleans.

>>> False/True

Output

Remember that division results in a float.

>>> True/False

Output

This was an exception that was raised. We will learn more about exceptions in a later lesson.

Modulus, Exponentiation, and Floor Division:

The same rules apply for modulus, exponentiation, and floor division as well.

>>> False%True
>>> True**False

Output

>>> False**False

Output

>>> 0//1

Try your own combinations like the one below.

>>> (True+True)*False+True

Output

b. Relational Operation

The relational operators we’ve learnt so far are >, <, >=, <=, !=, and ==. All of these apply to Boolean values.

We will show you a few examples; you should try the rest of them.

>>> False>True

Output

>>> False<=True

Output

Again, this takes the value of False to be 0, and that of True to be 1.

c. Bitwise Operation

Normally, the bitwise operators operate bit-by bit. For example, the following code ORs the bits of 2(010) and 5(101), and produces the result 7(111).

>>> 2|5

Output

But the bitwise operators also apply to Booleans. Let’s see how.

Bitwise & :

It returns True only if both values are True.

>>> True&False

Output

>>> True&True

Output

Since Booleans are single-bit, it’s equivalent to applying these operations on 0 and/or

Bitwise | :

It returns False only if both values are False.

>>> False|True

Output

Bitwise XOR (^) :

This returns True only if one value is True and one is False.

>>> False^True

Output

>>> False^False

Output

>>> True^True

Output

Binary 1’s Complement :

This calculates 1’s complement for True(1) and False(0).

>>> ~True

Output

>>> ~False

Output

Left-shift(<<) and Right-shift(>>) Operators :

As discussed earlier, these operators shift the value by specified number of bits left and right, respectively.

>>> False>>2
>>> True<<2

Output

True is 1. When shifted two places two the left, it results in 100, which is binary for 4. Hence, it returns 4.

d. Identity Operation

The identity operators ‘is’ and ‘is not’ apply to Booleans.

>>> False is False

Output

>>> False is 0

Output

e. Logical Operation

Finally, even the logical operators apply on Booleans.

>>> False and True

Output

This was all about the article on Python sets and booleans.

Python Interview Questions on Sets and Booleans

1. What is Boolean in Python?

2. How do you set a Boolean value in Python?

3. Give an example of a Python set and a Boolean?

4. How do you use Boolean in Python?

5. How do you check if a value is a Boolean in Python?

Conclusion

A Python set is an unordered bag of unique items, built for rapid membership tests. Put data inside curly braces and duplicates vanish automatically, leaving each element only once. This feature shines when cleaning lists of user IDs, tags, or sensor codes.

Because sets use hashing like dictionaries, the expressions if x in my_set or my_set.add(x) runs in constant time even for ten million items. Set math—union, intersection, difference—maps directly to operations in logic and search filters. Booleans, on the other hand, are the tiny twins True and False that steer program flow.

See you tomorrow. Hope you liked our article on Python sets and booleans.