R Recursive Function (Recursion) – A Complete Tutorial for Beginners!
FREE Online Courses: Click for Success, Learn for Free - Start Now!
In this R tutorial, we are going to cover the most interesting programming feature i.e. R recursive function. First of all, we will discuss the recursion concept, recursive function in R and different examples of it. Then we will also cover features and applications of R recursive function.
What is Recursion?
In a recursive function (recursion), function calls itself. In this, to solve the problems, we break the programs into smaller sub-programs.
For example:
4! = 4*3*2*1 = 24
This problem of finding factorial of 4 is been broken down into a sub-problem of multiplying the factorial of 3 with 4.
4! = 4*3
Or more generally,
n! = n*(n-1)!
Without this, the recursion will not end and will continue further.
Wait a second! Have you checked Matrix Function in R
What is Recursive Function in R?
Recursive functions call themselves. They break down the problem into the smallest possible components. The function() calls itself within the original function() on each of the smaller components. After this, the results will be put together to solve the original problem.
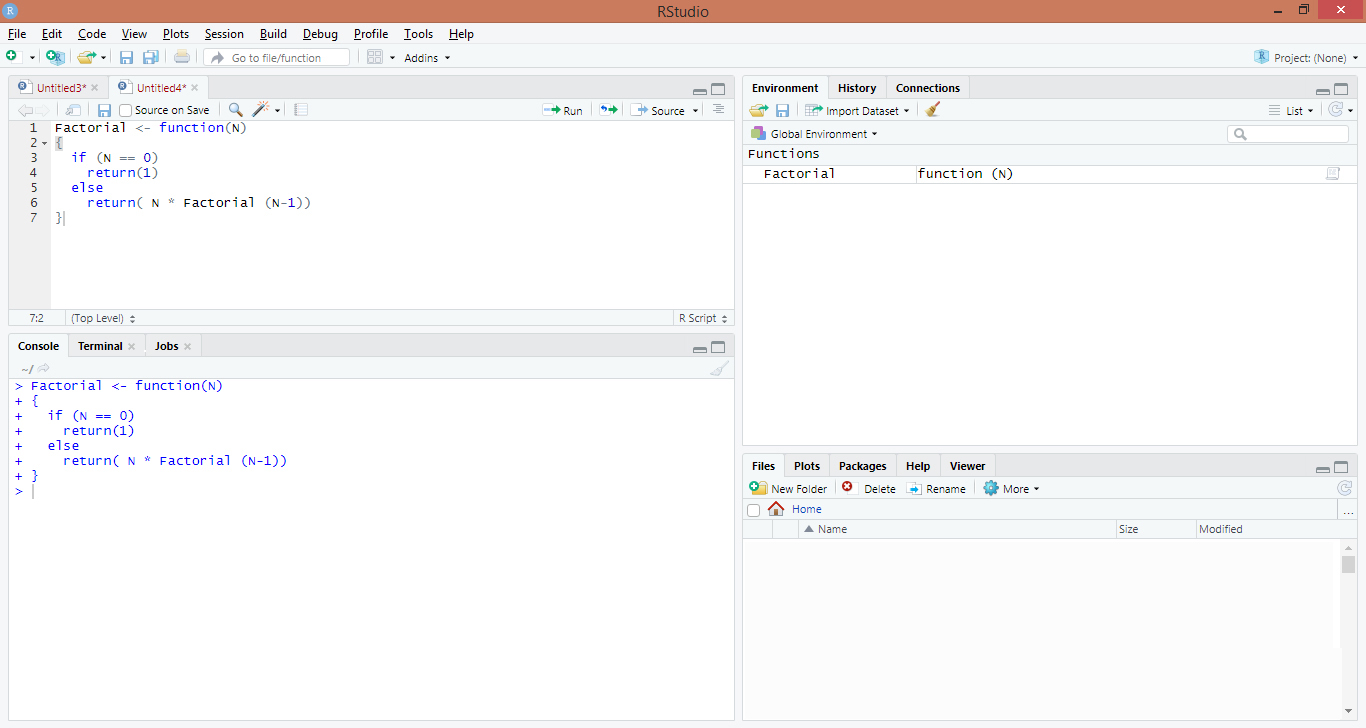
Factorial <- function(N)
{
if (N == 0)
return(1)
else
return( N * Factorial (N-1))
}Output:
Examples of R Recursive Function
1. Finding factorial of a number using the recursive function.
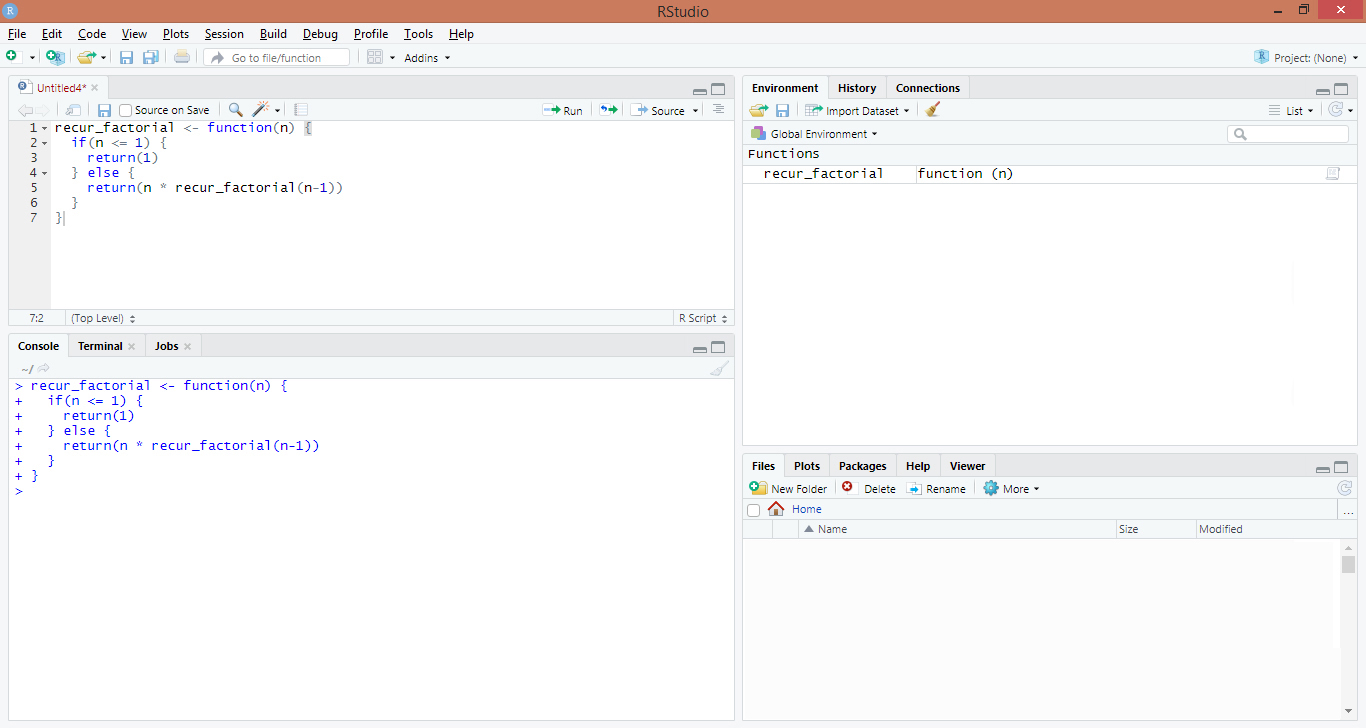
recur_factorial <- function(n) {
if(n <= 1) {
return(1)
} else {
return(n * recur_factorial(n-1))
}
}Output:
Here, recur_factorial() is used to compute the product up to that number. Let us suppose the user passes 4 to the function. Inside the recur_factorial(), the number 4 is been multiplied to the factorial of (4 – 1 = 3). 3 is been multiplied again to the factorial of (3 – 1 = 2). This goes on until the number reaches 1. Now, all previous functions of 2, 3 and 4 return the result one by one giving you the final result 1 * 2 * 3 * 4 which equals 24.
You should definitely check the Numeric and Character Functions in R
2. Finding the sum of natural numbers using the recursive function.
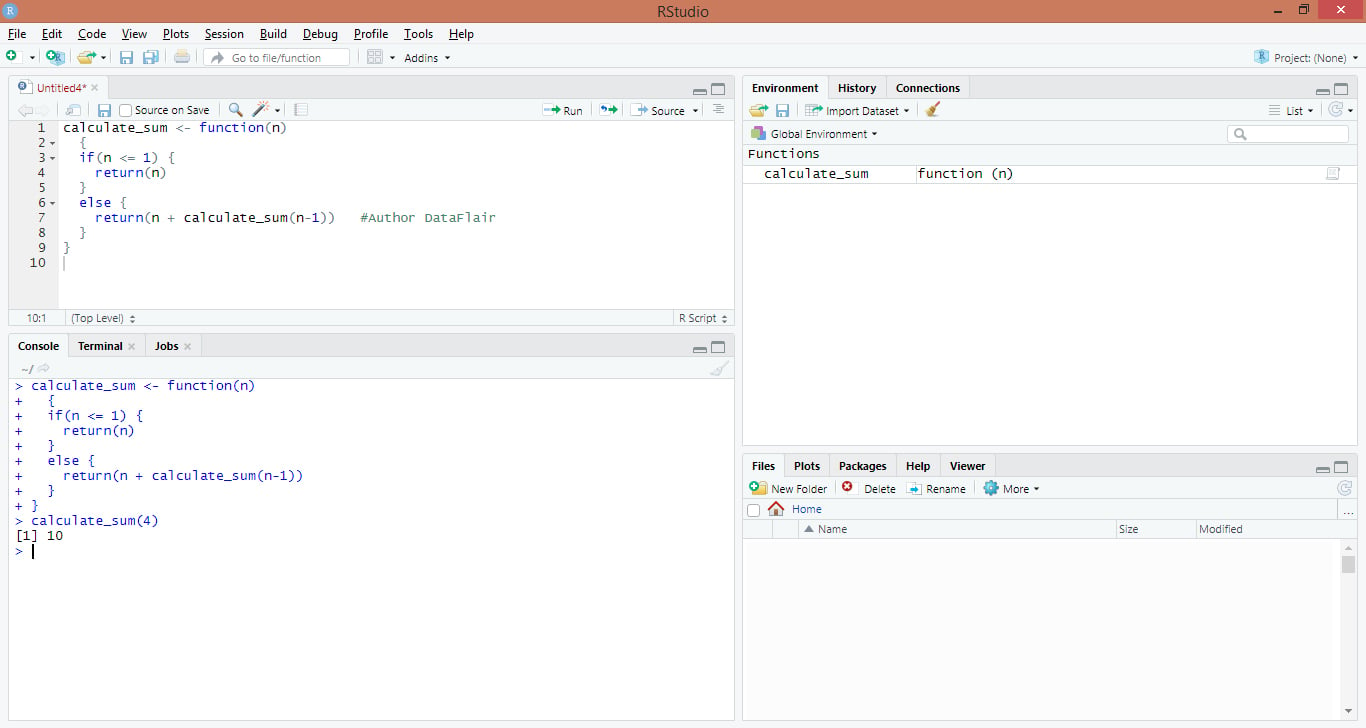
calculate_sum() <- function(n) {
if(n <= 1) {
return(n)
} else {
return(n + calculate_sum(n-1))
}
}Output:
Here, calculate_sum(n-1) is used to compute the addition up to that number. Let’s suppose the user passes 4 to the function. Inside the calculate_sum(n-1), the number is added to the sum of (4 – 1 = 3). Now, 4 is added to the sum of (n-1) i.e (4-1) = 3. It gives the final result as 4+(3+2+1) =10
3. Finding sum of series 1²+2²+3²+…..+n² using the recursive function.
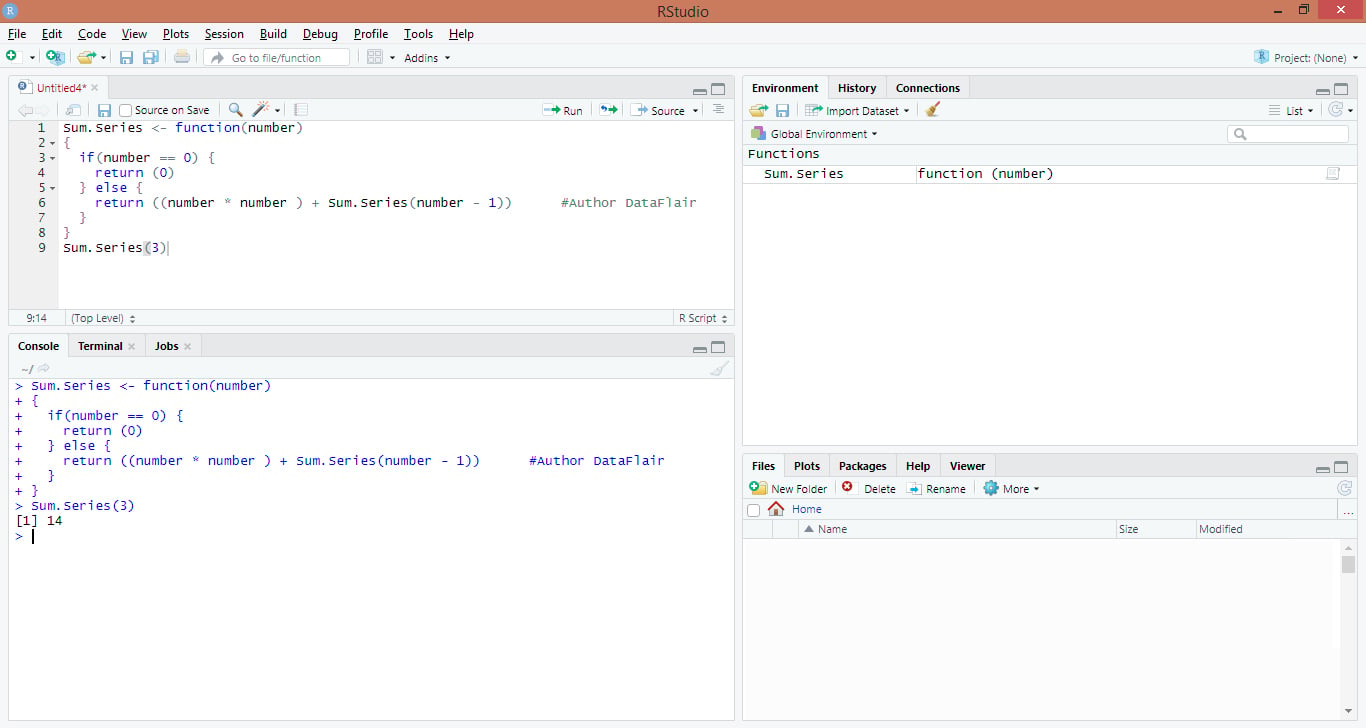
Sum.Series <- function(number)
{
if(number == 0) {
return (0)
} else {
return ((number * number ) + Sum.Series(number - 1))
}
}
Sum.Series(3)Output:
Let us divide the above expression for better understanding.
(number * number) = Multiplying the number
Sum.Series(number – 1) = Calling the same function with decremented value (decrease number by 1).
Recursion 1:
number = 4, which is greater than 0 so,
(number * number ) + Sum.Series(number – 1)
(4 * 4) + Sum.Series(4 – 1)
16 + Sum.Series(3)
Recursion 2:
number will become 3, which is greater than 0 so,
(number * number ) + Sum.Series(number – 1)
(3 * 3) + Sum.Series(3 – 1)
9 + Sum.Series(2)
Total will be 9 + 16 = 25
Recursion 3:
number will become 2, which is greater than 0 so,
(number * number ) + Sum.Series(number – 1)
(2 * 2) + Sum.Series(2 – 1)
4 + Sum.Series(1)
Total will be: 16 + 9 + 4 = 29
Recursion 4:
number will become 1, which is greater than 0 so,
(number * number ) + Sum.Series(number – 1)
(1 * 1) + Sum.Series(1 – 1)
1 + Sum.Series(0)
Total will be 16 +9 + 4 + 1 = 30
Recursion 5:
Number will become 0, which means the first if condition is true, so, it will exit from the function.
Final output will be 30.
Don’t forget to explore the Arguments in R
Key Features of R Recursion
Some major features of the R recursive function are:
- The use of recursion, often, makes the code shorter and it also looks clean.
- It is a simple solution for a few cases.
- It expresses in a function that calls itself.
Applications of R Recursion
After learning features of recursive function in R, now let’s discuss the applications of R recursive functions.
1. Dynamic Programming
It is the process to avoid re-computation. It is also an essential tool for statistical programming. There are two types of dynamic programming:
1.1. Bottom-up Dynamic Programming
- In this, we check the function starting with the smallest possible argument value.
- All computed values will be stored in an array.
1.2. Top-down Dynamic Programming
- Save each computed value as the final act of a recursive function.
- Check if pre-computed values exist as the first action.
2. Divide and Conquer Algorithms
- It is a common class of recursive function.
- Common features of this algorithm are process inputs, dividing the input into smaller portions, recursive call(s) process, at least one part.
- Recursion may sometimes occur before the input is been processed.
Summary
We studied about recursion, its features, and examples of the recursive function. In this tutorial, we have also learned about recursive functions which arise often in statistics and dynamic programming along with its type.
Get selected in your R interview with the Latest R Programming Interview Questions
Hope you liked this blog. If you have any queries about R recursive function, you can share with us using the comment section given below.
You give me 15 seconds I promise you best tutorials
Please share your happy experience on Google


Very informative
Wow, that was very useful. Simple, straightforward, yet very informative.
Thanks so much for this!
Many thanks. I am going to read all of these R tutorials
Hey Nguyen,
We are happy to help you. Do recommend us on Facebook and keep visiting DataFlair for further updates.